17 Jun 2021
I recently learned about bitonic sort networks, which are networks used for sorting numbers in parallel. A cool thing about them is that halfway through, the unordered sequence has been converted into a bitonic sequence, after which it is merged into a completely ordered sequence. [1]
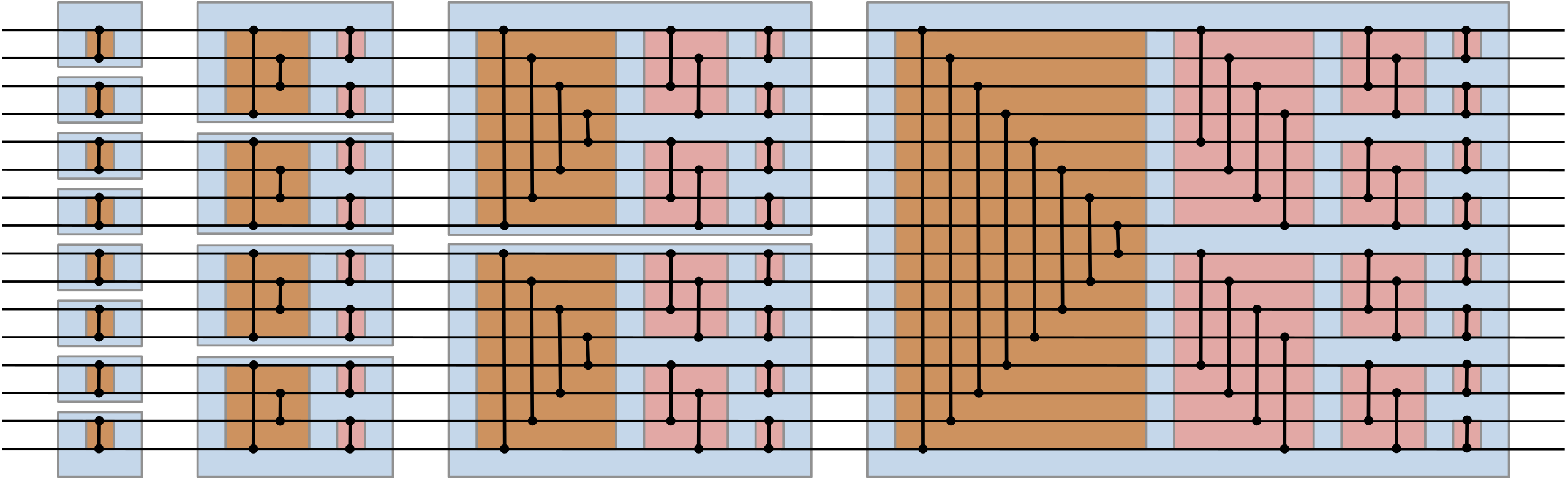
Here’s a picture of a 16-input bitonic sorter:
Each pair of junctions you see are doing something special:
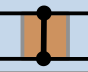
Two inputs enter in on the left. The minimum of the two emerges on the upper right, and maximum of the two emerges on the lower right.
PyRTL Implementation
One thing to notice about this network it’s essentially made up of smaller mini bitonic-networks connected together. If you look at the 16-input bitonic sorter image above, there are 16 blue squares, starting with 2-input blocks on the left and doubling to the largest 16-input block on the right. I smell recursion, and that’s exactly how I’m going to write it up in PyRTL.
Signed = False
def comp(a, b):
lt = pyrtl.signed_lt(a, b) if Signed else a < b
low = pyrtl.select(lt, a, b)
high = pyrtl.select(lt, b, a)
return low, high
def split(*args):
mid = len(args) // 2
return args[:mid], args[mid:]
def cleaner(*args):
upper, lower = split(*args)
res = [comp(*t) for t in zip(upper, lower)]
new_upper = tuple(t[0] for t in res)
new_lower = tuple(t[1] for t in res)
return new_upper, new_lower
def crossover(*args):
upper, lower = split(*args)
res = [comp(*t) for t in zip(upper, lower[::-1])]
new_upper = tuple(t[0] for t in res)
new_lower = tuple(t[1] for t in res[::-1])
return new_upper, new_lower
def merge_network(*args):
if len(args) == 1:
return args
upper, lower = cleaner(*args)
return merge_network(*upper) + merge_network(*lower)
def block(*args):
upper, lower = crossover(*args)
if len(upper + lower) == 2:
return upper + lower
return merge_network(*upper) + merge_network(*lower)
def bitonic_helper(*args):
if len(args) == 1:
return args
else:
upper, lower = split(*args)
new_upper = bitonic_helper(*upper)
new_lower = bitonic_helper(*lower)
return block(*new_upper + new_lower)
def bitonic_sort(*args):
if len(args) == 0:
raise Exception("bitonic_sort requires at least one argument to sort")
if len(args) & (len(args) - 1) != 0:
raise Exception("number of arguments to bitonic_sort must be a power of 2")
return bitonic_helper(*args)We can simulate it with completely unordered inputs:
>>> pyrtl.reset_working_block()
>>>
>>> args = pyrtl.input_list('a1 a2 a3 a4 a5 a6 a7 a8', 8)
>>> c1, c2, c3, c4, c5, c6, c7, c8 = bitonic_sort(*args)
>>>
>>> pyrtl.probe(c1, 'c1')
>>> pyrtl.probe(c2, 'c2')
>>> pyrtl.probe(c3, 'c3')
>>> pyrtl.probe(c4, 'c4')
>>> pyrtl.probe(c5, 'c5')
>>> pyrtl.probe(c6, 'c6')
>>> pyrtl.probe(c7, 'c7')
>>> pyrtl.probe(c8, 'c8')
>>>
>>> sim = pyrtl.Simulation()
>>> sim.step({
>>> 'a1': 32, 'a2': 2, 'a3': 98, 'a4': 102,
>>> 'a5': 88, 'a6': 97, 'a7': 107, 'a8': 1,
>>> })
>>>
>>> ordered = [1, 2, 32, 88, 97, 98, 102, 107]
>>> for ix in range(8):
>>> assert sim.inspect(f'c{ix+1}') == ordered[ix]This succeeds (no assertions fail)!
Now, the best part: seeing its visualization:
>>> with open("bitonic_sorter_pyrtl_8.svg", "w") as f:
>>> pyrtl.output_to_svg(f)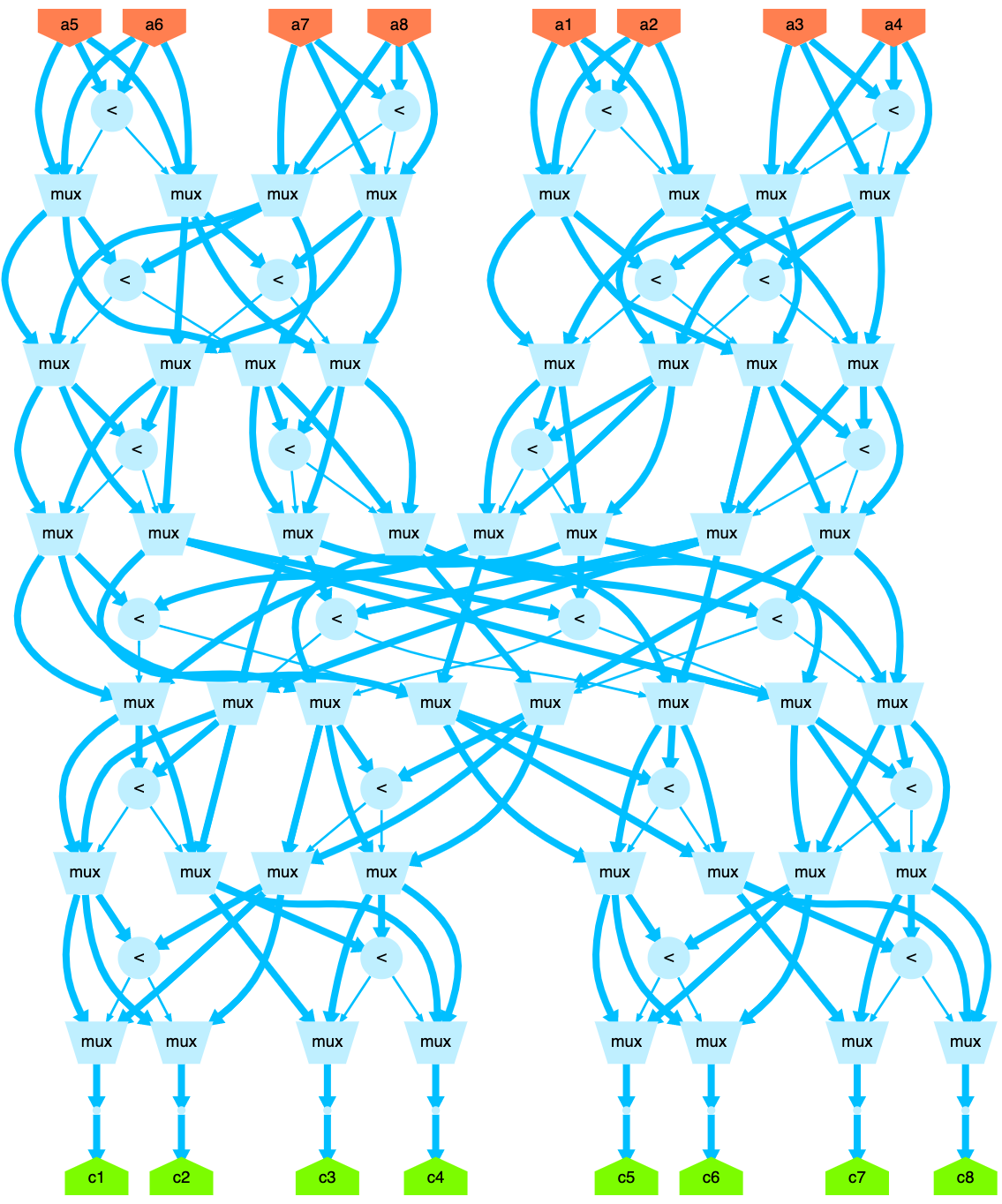
This is the 8-input version, which is equivalent to the upper-left quadrant of the original image we looked at the beginning of this post (turned 90 degrees clockwise). The most important thing to notice is that there are 24 "less-than" logic nets, which is the same number of comparison junctions found in 8-input section of the original image; that means we’ve implemented the minimal version of this sorting network.
Background Information
A well-cited paper on sorting networks, including the aforementioned bitonic sorting network, is "Sorting networks and their applications" by K. E. Batcher (1968). Look there if you want more of the theoretical underpinnings about why it works.
1. "Bitonic" means that the sequence is monotically non-{decreasing, increasing}, modulo some circular shift.